【電気回路の問題】中央の5Ωがあるのに無視できる?合成抵抗の考え方を解説
今回は、少しトリッキーな電気回路の問題を扱います。
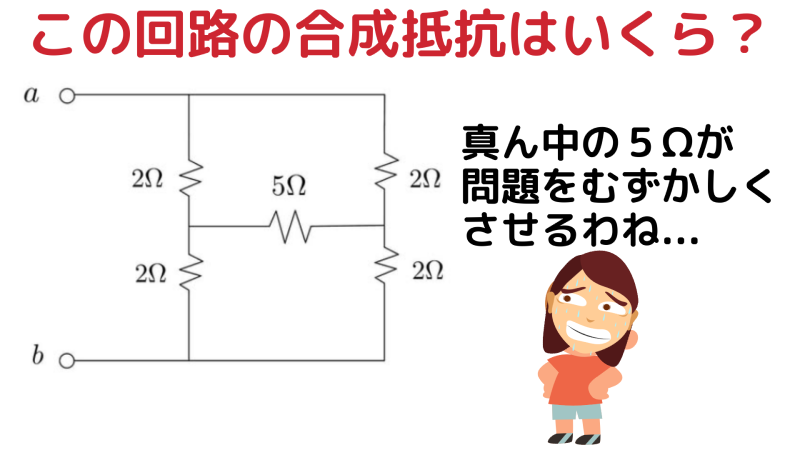
A と B の 2 点間に、左右対称に 2Ω+2Ω の直列抵抗が並列につながっており、さらにその左右の中間を 5Ω の抵抗が橋渡しするように接続されています。
一見すると、この 真ん中の 5Ω の存在が計算を難しくしているように見えます。
しかし実は、この 5Ω は“無視してよい”場合があります。 なぜそんなことが起こるのか、順を追って説明します。
回路の構成を整理する

- 左側:2Ω → 2Ω の直列(合計 4Ω)
- 右側:2Ω → 2Ω の直列(合計 4Ω)
- 左右の中点同士を 5Ω が接続
- 左右の 4Ω 同士は A–B 間で並列につながっている
見た目は複雑ですが、左右が完全に対称である点が重要です。
ある人の考え方:5Ωを無視して計算してみる
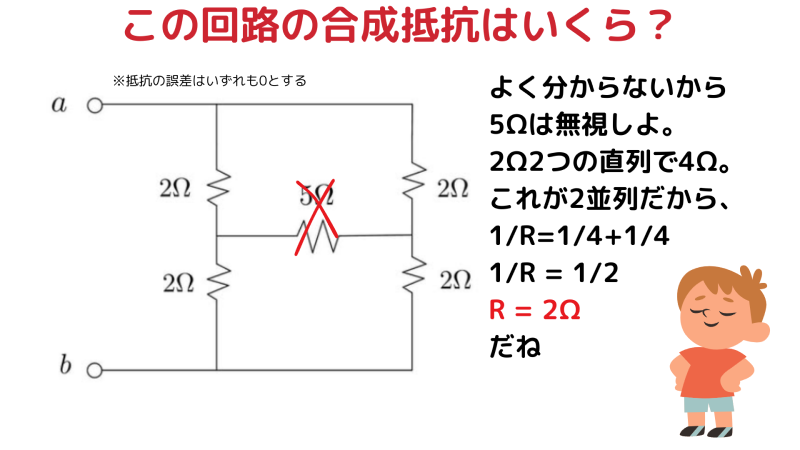
「5Ω があると難しいので、いったん無視してみる」という発想です。
- 左側:4Ω
- 右側:4Ω
- 4Ω と 4Ω の並列 → 合成抵抗は 2Ω
実際、この問題の答えは 2Ω なので、この考え方は正しいことになります。
では、なぜ 5Ω を無視してもよいのでしょうか。
5Ω の両端の電位差を考える
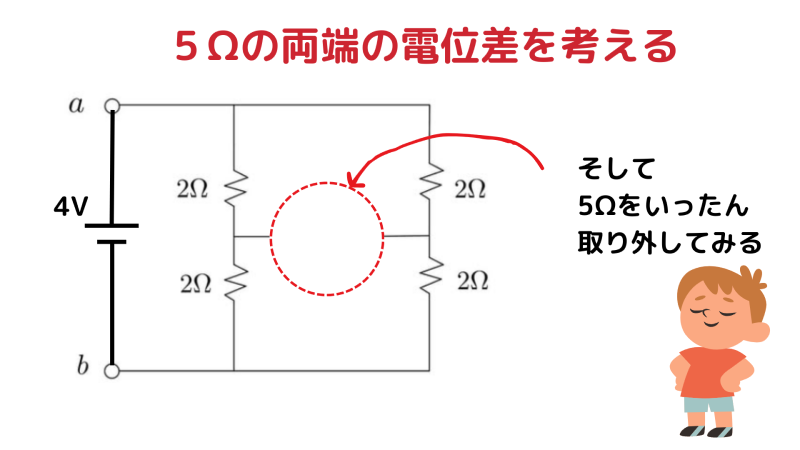
理解のポイントは 5Ω の両端の電位が同じになるという点です。
説明のために、A–B 間に 4V の電源をつないだと仮定します。
さらに、5Ω を一度取り外して考えます。
右側のループを流れる電流
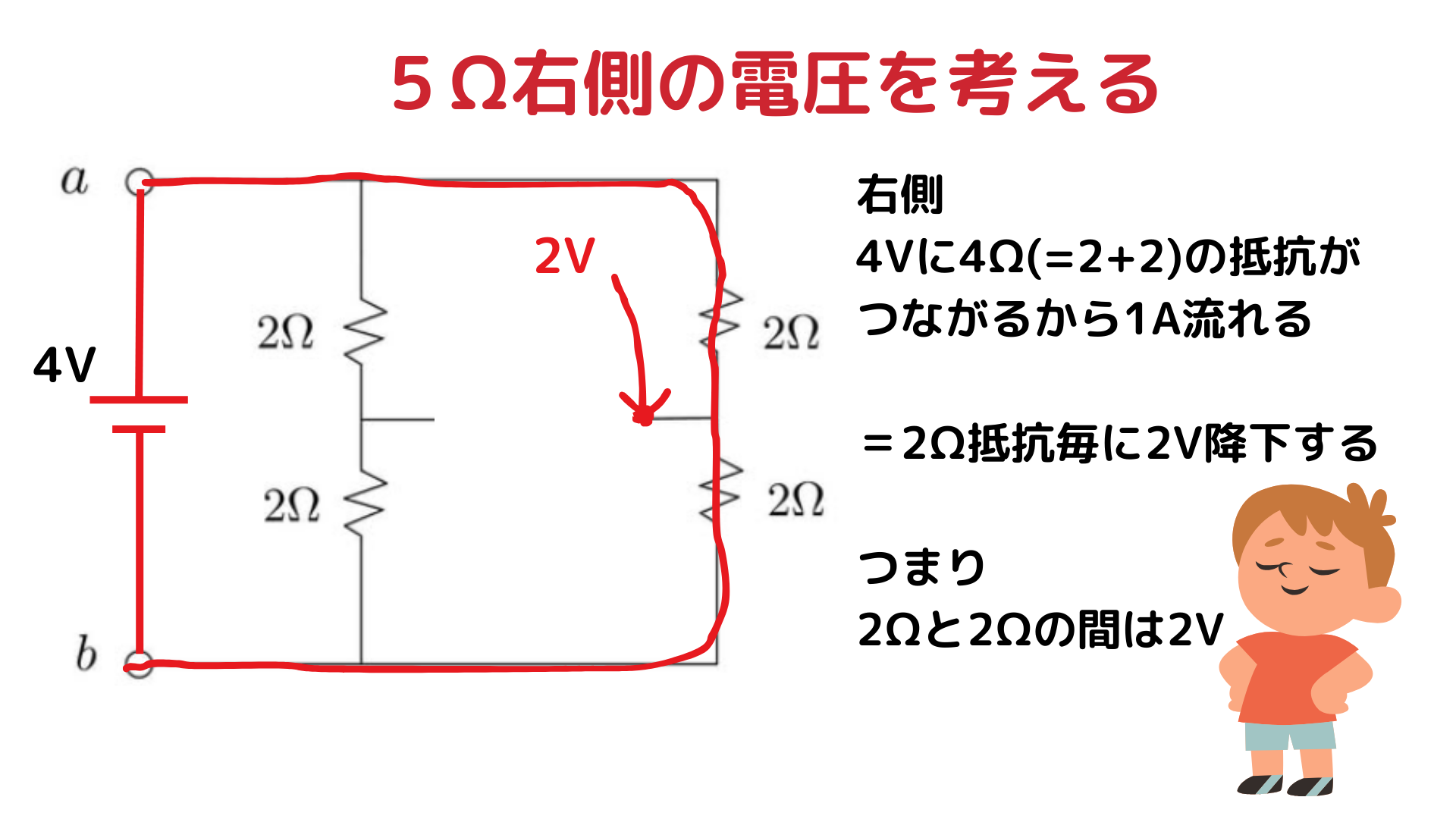
右側の抵抗は 2Ω+2Ω=4Ω。 4V の電源がつながっているので、流れる電流は
電圧降下は以下の通り:
- 1つ目の 2Ω:2V 下がる
- 2つ目の 2Ω:さらに 2V 下がる → 0V
つまり、右側の 2Ω と 2Ω の間の電位は 2V になります。
左側のループも同様
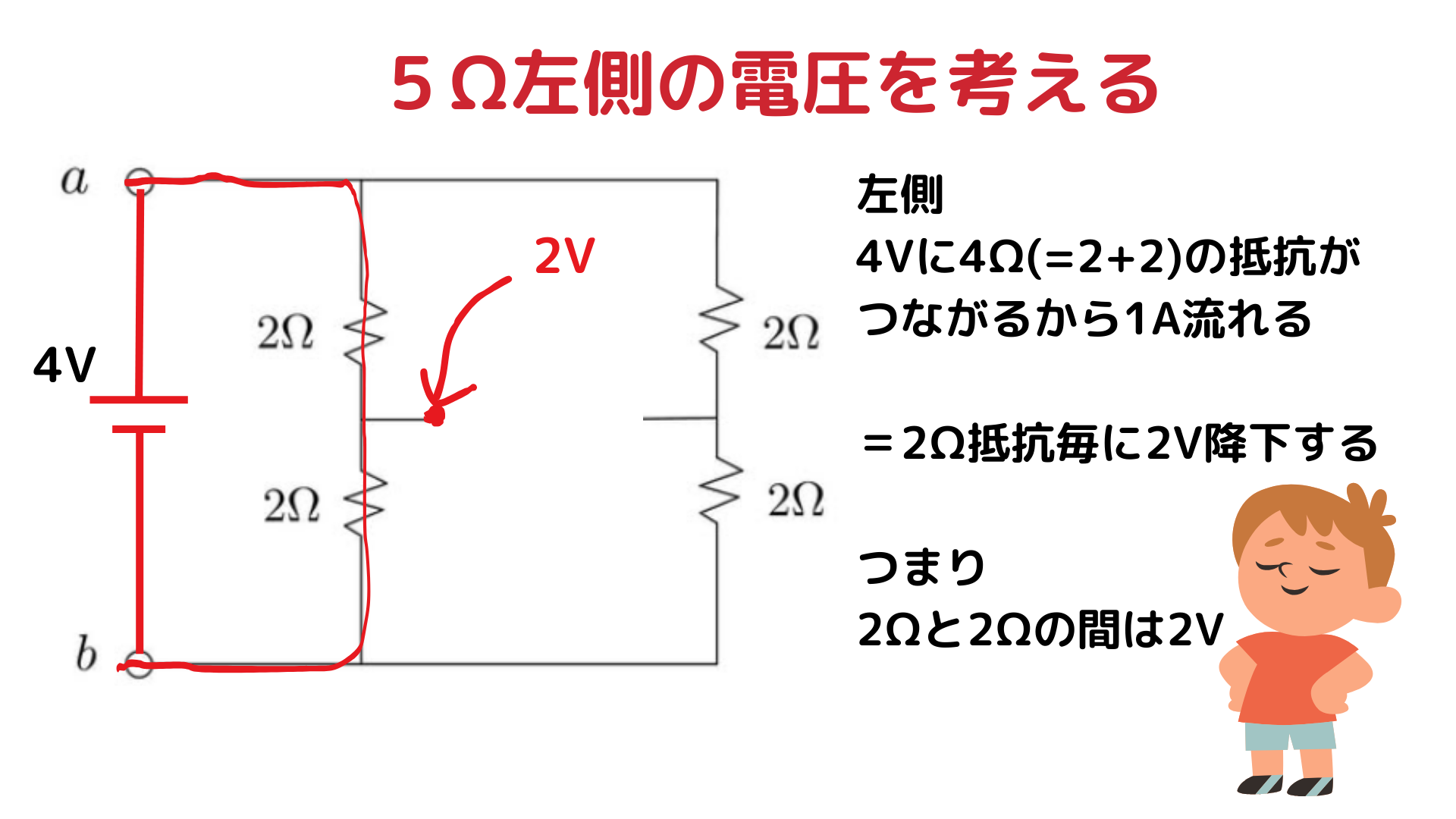
左側もまったく同じ構成なので、同じように 1A が流れ、 中点の電位は 2V になります。
5Ω の両端の電位差は 0V → 電流は流れない
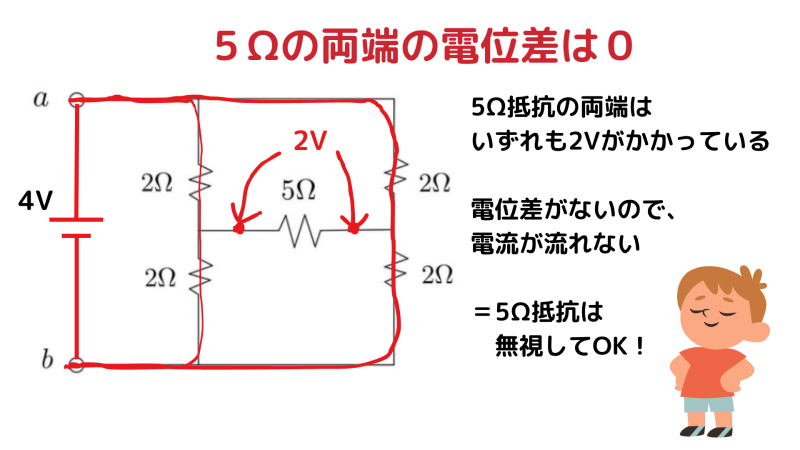
左右の中点はどちらも 2V。 つまり、5Ω の両端は 2V – 2V = 0V。
電位差が 0V なので、5Ω には 電流が流れません。
電流が流れない抵抗は、回路的には「存在しない」のと同じです。 したがって、5Ω を無視してよいという結論になります。
結果:合成抵抗は 2Ω
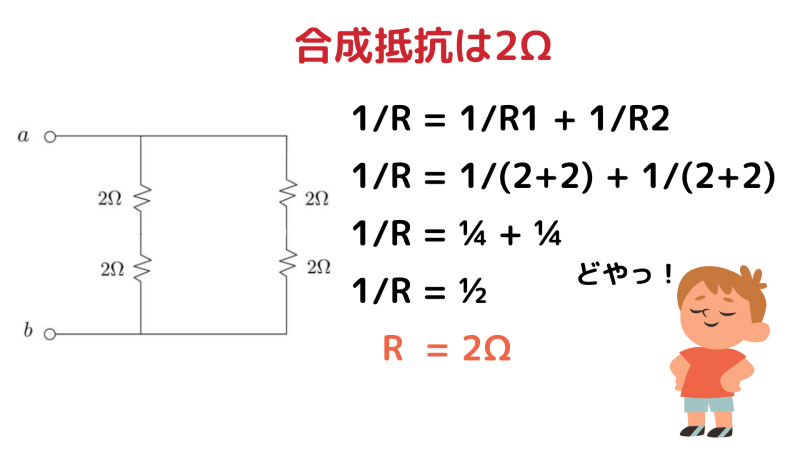
5Ω を取り除いた形で考えると、
- 左:4Ω
- 右:4Ω
- 並列 → 合成抵抗は 2Ω
これが答えです。
では、左右の抵抗値が対称でない場合は?
今回の例では左右が完全に対称だったため、5Ω の両端の電位が一致し、電流が流れませんでした。
しかし、例えば片側の 2Ω を 3Ω に変更すると、左右の電位バランスが崩れます。
すると 5Ω の両端に電位差が生じ、電流が流れるようになります。
この場合は 5Ω を無視できず、別の計算方法が必要になります。
その解き方については、次回の記事で紹介します。
まとめ
- 左右が対称な回路では、中点の電位が一致する
- そのため、中央の抵抗には電流が流れない
- 電流が流れない抵抗は無視できる
- 結果として、合成抵抗は 2Ω
電気回路の対称性を利用すると、複雑に見える問題もシンプルに解けるようになります。
