初心者でもわかるキルヒホッフの法則｜3つのループで電流を求める実践例

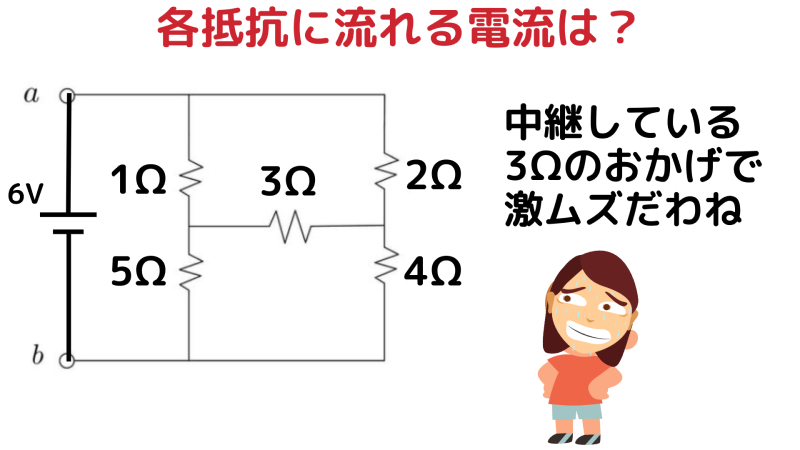
複雑に見える電気回路でも、オームの法則とキルヒホッフの法則を使えば確実に解けます。
今回は、6V の直流電源と 1Ω・5Ω・2Ω・4Ω・3Ω の抵抗で構成された回路について、 各抵抗に流れる電流を求める問題を扱います。

回路の構成

6V の電源から以下のように抵抗が接続されています。

• 左側：1Ω → 5Ω
• 右側：2Ω → 4Ω
• 左右の途中をつなぐ：3Ω

一見すると単純な並列回路に見えますが、中央の 3Ω が左右の回路を結んでいるため、電流が分岐・合流する複雑な回路になっています。

ある人の誤った考え方

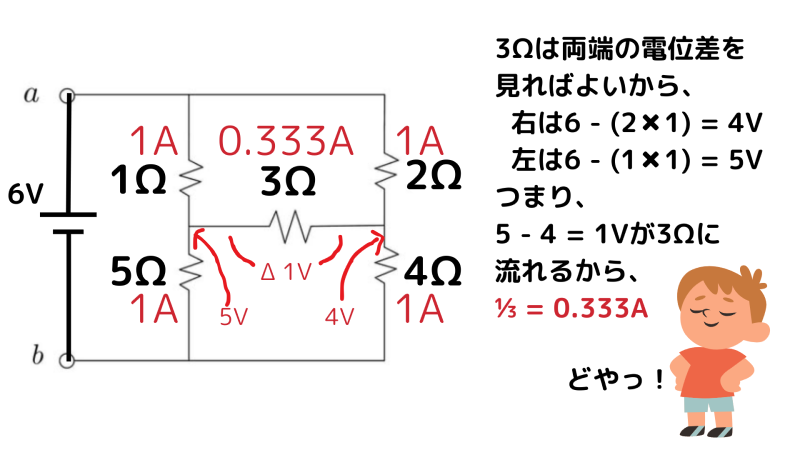
ある人は次のように考えました。

• 左側（1Ω + 5Ω = 6Ω）に 6V → 1A
• 右側（2Ω + 4Ω = 6Ω）に 6V → 1A
• よって左右の抵抗にはすべて 1A が流れる
• 中央 3Ω の電圧差は
  • 左：6V − 1A×1Ω = 5V
  • 右：6V − 1A×2Ω = 4V → 差 1V → 3Ωに 1/3A

一見正しそうですが、この考え方には重要な欠点があります。

正しい考え方：電流の経路（ループ）をすべて考える

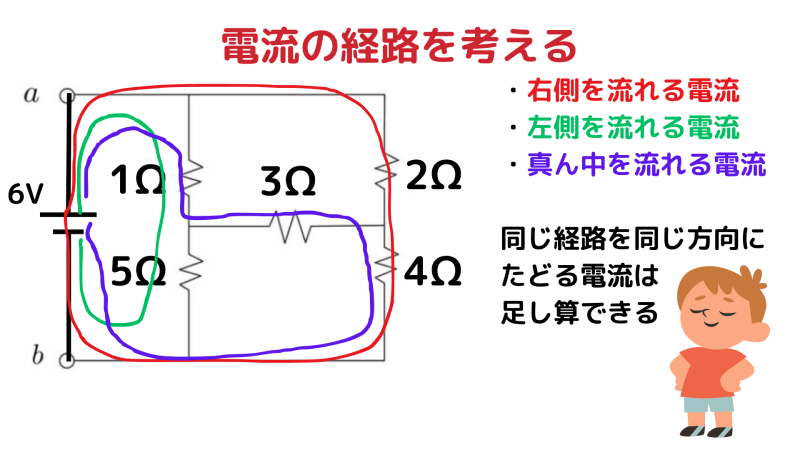
この回路には、実は次の 3つの独立したループ が存在します。

1. 外側を回るループ（赤）
2. 左側のループ（緑）
3. 1Ω → 3Ω → 4Ω を通るループ（紫）

キルヒホッフの法則では、 同じ経路を同じ方向に流れる電流は足し合わせてよい というルールがあります。

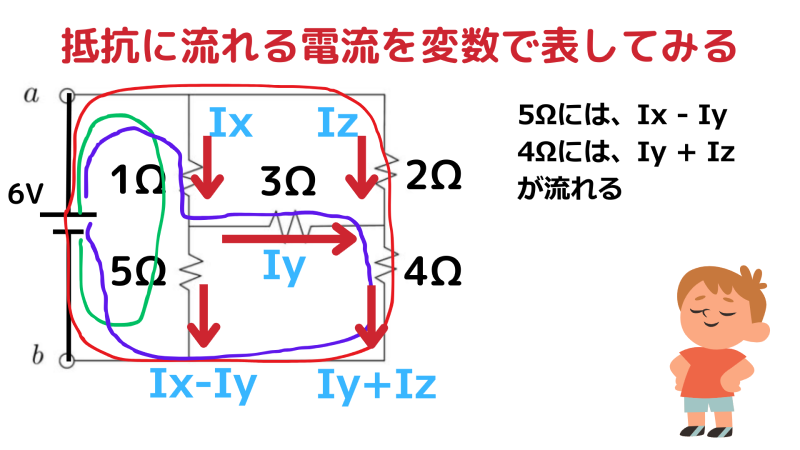
そこで、次のように電流を定義します。

• 1Ω を流れる電流：$I_x$
• 3Ω を左→右に流れる電流：$I_y$
• 2Ω を流れる電流：$I_z$

このとき、5Ω と 4Ω を流れる電流は次のように表せます。

• 5Ω：もともと $I_x$ が流れるが、途中で $I_y$ が分岐する → $I_x-I_y$
• 4Ω：もともと $I_z$ が流れるが、途中で $I_y$ が合流する → $I_y+I_z$

各ループにキルヒホッフの法則を適用する

① 外側のループ（赤）

$$6=2I_z+4(I_y+I_z)$$

② 左側のループ（緑）

$$6=I_x+5(I_x-I_y)$$

③ 1Ω → 3Ω → 4Ω のループ（紫）

$$6=I_x+3I_y+4(I_y+I_z)$$

これら 3 本の式を連立して解きます。

連立方程式を解いた結果

$$I_x=1.161\text{ A}$$

$$I_y=0.193\text{ A}$$

$$I_z=0.871\text{ A}$$

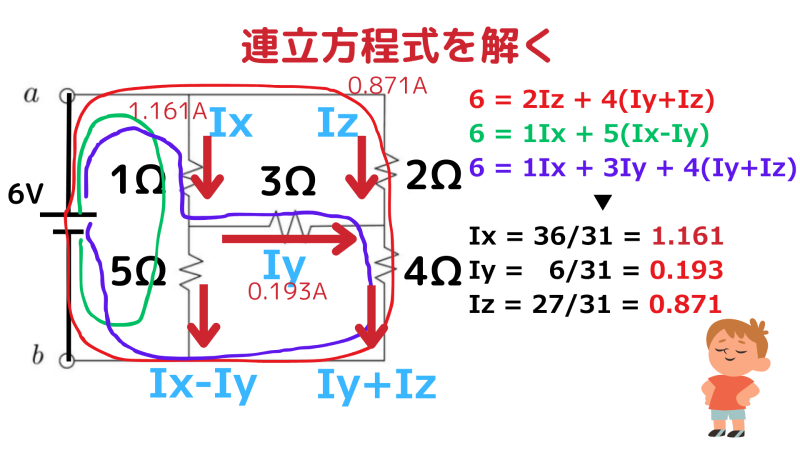
各抵抗に流れる電流

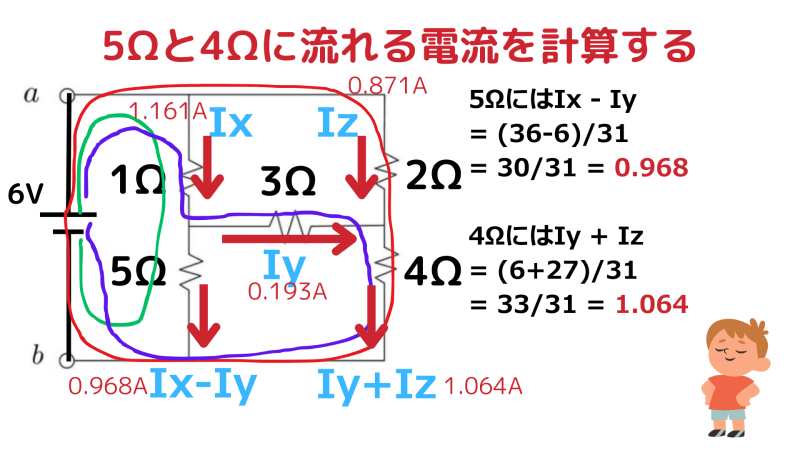
求めた電流を使って、5Ω と 4Ω の電流も計算できます。

• 5Ω

$$I_x-I_y=1.161-0.193=0.968\text{ A}$$

• 4Ω

$$I_y+I_z=0.193+0.871=1.064\text{ A}$$

3Ω の電流の向きについて

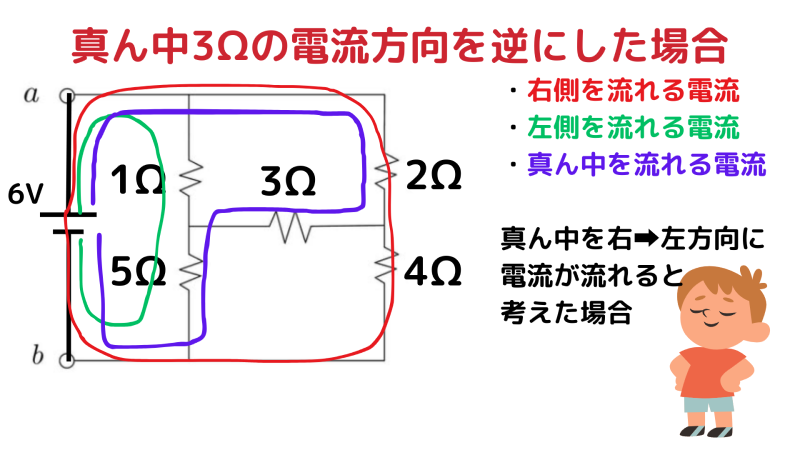
3Ω を流れる電流 $I_y$ の向きは、最初に仮定した「左→右」で正しかったことが、 計算結果（正の値）からわかります。

もし逆向きに仮定して式を立てると、

$$I_y=-0.193\text{ A}$$

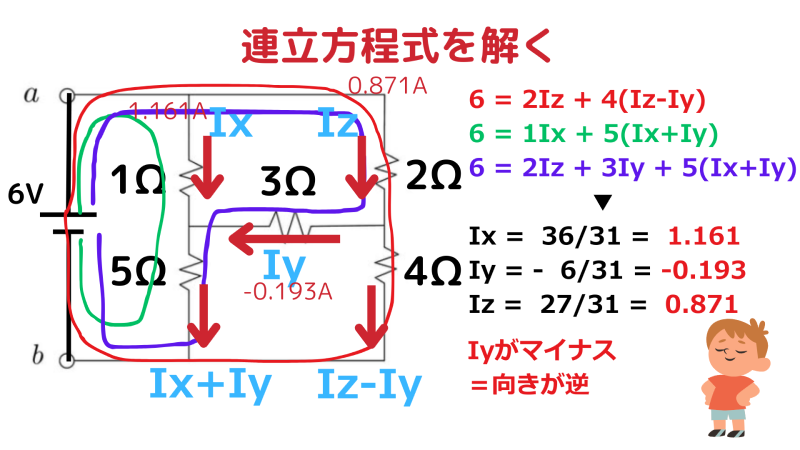
となり、負号が「向きが逆だった」ことを示すだけで、 最終的な電流値は同じになります。

まとめ

この問題は、見た目以上に複雑な回路ですが、

• オームの法則
• キルヒホッフの法則（電圧則・電流則）
• ループ電流法

を使えば確実に解けます。

複雑な回路ほど、 「どの電流がどの経路を通るか」を丁寧に整理することが重要です。